Step Polymerisations
One of the processes to make polymers is called step polymerisation and this process used to be called a condensation polymerisation due to the formation small byproduct or condensate. In this section, we will see the chemistry behind step polymerisations especially in polyesterification and its kinetics.
To begin with, let consider esterification process first. The esterification depends on the monofunctionality and it will give low molecular weight products.
On the other hand, bifunctional of carboxylic acids and alcohols would give polymers. Furthermore, a cross-linked system could be formed from multifunctional monomers.
In step polymerisation, the repeat unit linkage is not necessary an ester group, but it could be polyamide, polyurethane, polyurea or even polycarbonate.
Understanding the kinetics of step polymerisation is slightly tricky due to the nature of the reaction. In polymerisation, monomers can react to form dimers, trimers and so on, but the formed dimers and longer chain could react with each others which would give complexity to the reaction. In the other words, all species in the reaction are capable to do reaction which means every reaction has own rate constant. Therefore, in this kinetics study there are two assumptions that can be used to simplify the problem which are reactivity of functional group are independent of molecular size and no side reactions or impurities.
Now, considering the reaction of diol and diacid to form a polyester which is catalysed by an acid HA.
The reaction proceeds via two steps mechanism where the first step involving activation of carbonyl group by protonation. This step is reversible and fast. The second step is the esterification of activated carbonyl and this step is the slow which implies the rate-limiting step (r.l.s.).
This means the overall kinetics depend on the second slow step.
However, from equilibrium shown in step 1 that
from this equation, the term of activated carbonyl can be replaced to observable quantity as shown below.
Then, by considering the ionisation equilibrium of acid catalyst,
the rate law can be written as
Besides that, in the absence of external catalyst, i.e. HA = RCOOH, the rate law becomes
This rate law shows that it is second order rate law with respect to RCOOH and first law to ROH. Furthermore, this means the rate law can be monitored from the depletion of RCOOH against time using titration method.
Then, if diol and diacid have stoichiometry of 1:1, then [acid] = [ROH] = [C]. Thus, the rate law for self-catalysed polyesterification is
which then can be integrated to give a time-dependent rate law as shown below.
A parameter can be introduced which is the fractional extent of reaction p where p can be between 0 to 1. The parameter p can be defined as
where [C]0 is the initial concentration of acid. Then, the rate law becomes
which means a plot of 1/(1-p)2 against t should give a linear plot. The example below is a polyesterification of adipic acid and diethylene glycol.
From the graph, it shows a linear relationship at 83 - 90% conversion with deviations at low and high p. At low p, the deviation might come from the changes in solvency while increased in viscosity or depolymerisation might cause the deviation at high p.
When the polymerisation is catalysed by strong acid such as H2SO4 or 4-toluenesulfonic acid (TsOH), then concentration of HA is constant since catalyst is unchanged at the end of reaction. Hence, for acid-catalysed polyesterification, assuming the stoichiometry of diol and diacid is 1:1, the rate equation is modified to
which means a plot of 1/(1-p) against time should give a linear plot.
The degree of polymerisation in polyesterification can be described as the ratio of initial and final concentration of C which means the reciprocal of (1-p).
Hence, Mn can be calculated as follow.
This equation is known as Carothers equation which was proposed by Wallace Carothers, the inventor of Nylon. From those equations above, this implies that to achieve high MW polyesters, it requires a reaction to be near completion or p close to 1.
For example, when p = 0.5, Dp is only 2 or dimer; then when p = 0.9, Dp is only 10. A low MW polyester with Dp = 50, it needs p = 0.98. Then, for high MW such as Dp is 100 or 1000, p needs to be 0.99 and 0,999 consecutively. This means step polymerisation builds up the mass slowly.
Furthermore, Mw of polyesterification can be calculated as
so polydispersity index (PDI) can be calculated as shown below.
In building up high MW polyesters, there are several factors that can influence its MW. Firstly, the presence of impurities such as monofunctional monomers can severly limit the Dp. Furthermore, side-reactions would give the same effect. Secondly, achieving high MW needs to maximise p by using high temperature and long reaction times. Besides that, driving the esterification equilibrium to the right side can be done to get polyester by removing volatile condensate such water. Therefore, it needs an irreversible polyesterification reaction to achieve high MW. Lastly, non-stoichiometry of bifunctional monomers can also reduce Dp which means the monomers need to be as close as 1:1. This also means a high purity monomers are needed.
To begin with, let consider esterification process first. The esterification depends on the monofunctionality and it will give low molecular weight products.
Understanding the kinetics of step polymerisation is slightly tricky due to the nature of the reaction. In polymerisation, monomers can react to form dimers, trimers and so on, but the formed dimers and longer chain could react with each others which would give complexity to the reaction. In the other words, all species in the reaction are capable to do reaction which means every reaction has own rate constant. Therefore, in this kinetics study there are two assumptions that can be used to simplify the problem which are reactivity of functional group are independent of molecular size and no side reactions or impurities.
Now, considering the reaction of diol and diacid to form a polyester which is catalysed by an acid HA.
Besides that, in the absence of external catalyst, i.e. HA = RCOOH, the rate law becomes
Then, if diol and diacid have stoichiometry of 1:1, then [acid] = [ROH] = [C]. Thus, the rate law for self-catalysed polyesterification is
When the polymerisation is catalysed by strong acid such as H2SO4 or 4-toluenesulfonic acid (TsOH), then concentration of HA is constant since catalyst is unchanged at the end of reaction. Hence, for acid-catalysed polyesterification, assuming the stoichiometry of diol and diacid is 1:1, the rate equation is modified to
The degree of polymerisation in polyesterification can be described as the ratio of initial and final concentration of C which means the reciprocal of (1-p).
Furthermore, Mw of polyesterification can be calculated as
In building up high MW polyesters, there are several factors that can influence its MW. Firstly, the presence of impurities such as monofunctional monomers can severly limit the Dp. Furthermore, side-reactions would give the same effect. Secondly, achieving high MW needs to maximise p by using high temperature and long reaction times. Besides that, driving the esterification equilibrium to the right side can be done to get polyester by removing volatile condensate such water. Therefore, it needs an irreversible polyesterification reaction to achieve high MW. Lastly, non-stoichiometry of bifunctional monomers can also reduce Dp which means the monomers need to be as close as 1:1. This also means a high purity monomers are needed.
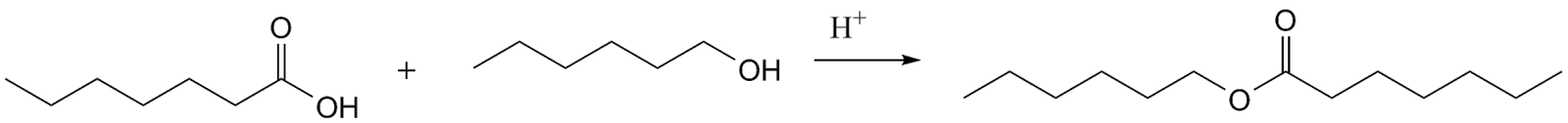
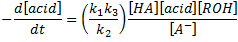
Comments