In this section, we will have a discussion for one of the consequences of crystal splitting (CFSE) stabilisation energy which is observed in a spectrum. In this section, we will explain some unique characteristics of complex compound's absorption spectrum. Furthermore, we will also see Jahn-Teller distortion which gives the unique pattern of absorption spectrum of a complex compound.
In the previous section of crystal field theory, we briefly discussed how CFSE (either ∆o or ∆tet) is influenced by the metal centre ion and the ligands. The CFSE increases at higher oxidation state and lower row of metal in the periodic table whereas increasing CFSE is also affected by the ligands of strong field ligands. As most of us acknowledge, the absorption spectrum of an atom is discrete since electrons are excited into certain energy level. However, the absorption spectrum of a complex compound (e.g. [Ti(OH2)6]3+) is a broad spectrum with a peak in visible region in most of the case.
 |
| The absorption spectrum of [Ti(OH2)6]3+ |
The highest peak corresponds to the value ∆o of the complex compound, in this example is [Ti(OH2)6]3+. Therefore, ∆o can be calculated by using this equation below,
where E corresponds to
∆o (J mol
-1),
h is the Planck's constant (6.626 x
10-34 J s),
c is the speed of light (approximately 3.00 x
10-34 m s
-1), is Avogadro's number (6.022 x
1023 mol
-1)and
λ is the wavelength of the highest peak (m). However, in the spectrum above, the spectrum has a distinguish characteristic such as the broad peak and the "shoulder, as well a high absorption in the UV region where we will explain it later.
 |
| Characteristics of absorption spectrum of complex compounds |
Firstly, we deal with the broad peak in the spectrum where electronic transitions are fast compared to molecular motions. The molecules is not a static object but it is a dynamic where molecules will be vibrating at any particular instant, so there will be a range of Ti-O distances rather than just one. Besides that, at any particular instant there will be a range of
∆o values and hence a range of transition energies which means we will see a broad peak.
Besides that, we also see an absorption spectrum at UV region and this absorption corresponds to charge transfer absorption. Charge transfer is when ligands with extra lone pairs can donate them into empty metal orbitals and usually occur in the UV but can stray into the visible region and can lead to very strong colour e.g.
KMnO4 [Mn(VIII) is d
0].
 |
| Charge transfer in complex compounds |
Before we move further, a big question where the spectrum comes from. The spectrum of complex compounds comes from the electronic transition which is limited by rules, one of it is Laporte selection rule. The Laporte selection rule says that transitions from centrosymmetric to centrosymmetric (or non-centrosymmetric to non-centrosymmetric) are forbidden and this means that a transition from the
t2g to
eg should not occur. However, molecular vibrations mean that a certain proportion of molecules will lose their centre of symmetry at any instant and can thus undergo the transition. Besides that, in the transitions electrons cannot change their spin state when they undergo
d-d transitions. One of the example is in high spin d
5 octahedral complexes have very pale colours or even colourless such as in
[Mn(OH2)6]2+.
 |
| Forbidden transition |
Another unique characteristic of an absorption spectrum of complex compound is it has a "shoulder" at shorter wavelength absorption. For this case, let consider something different such as high spin d
4 and we want to put the 4th electron. The fourth electron can have 2 possibilities, at
dx2-y2 or
dz2, but does it really matter where the electron is?
Firstly, if we consider the 4th electron in
dz2, so the ligands on the z axis feel extra repulsion and moves out a bit that makes ligands on the x and y axes feel less so can move in a bit. Therefore, we get a distorted octahedral structure which has 2 long bonds and 4 short ones and this is called tetragonal elongation. This distortion changes the splitting in octahedral splitting where all the orbitals with a z component are stabilised and the ones without are destabilised. Furthermore, the stabilisation energy of this distortion (
δ1 and
δ2) are much smaller than
∆o, just a few kJ mol
-1.
 |
| Tetragonal elongation |
Now, if we consider the 4th electron in
dx2-y2, so the ligands on the x and y axes feel extra repulsion and move out a bit whereas the ligands on the z axes feel less so can move in a bit. Then, in this case we have a distorted octahedral structure with 4 long bonds and 2 short bonds and this is known as tetragonal compression. Therefore, in this distortion the orbitals in xy plane are stabilised but the others are destabilised.
 |
| tetragonal compression |
This distortion was observed by H.A. Jahn and E. Teller 1937 which stated that a molecule in a degenerate electronic state will undergo a geometrical distortion so as to remove the degeneracy. This means, in our d
4 system we had a choice of two orbitals of the same energy which was a degenerate state. Then, after doing our distortion they were not degenerate any longer, so the degeneracy was successfully removed.
If we consider again our d
1 system of
[Ti(OH2)6]3+ and let consider the tetragonal compression first, so we have
From the splitting above, we no longer have a choice of where to put our electron, so the degeneracy has been successfully removed and the complex have gained 2/3
δ2 of extra stabilisation energy. Now, if we consider the tetragonal elongation we have
and we still have a choice of where to put our electron, so the degeneracy has not been successfully removed and the complex have only gained 1/3
δ2 of extra stabilisation energy. Hence, this distortion does not work so
[Ti(OH2)6]3+ could only has tetragonal elongation.
We could also predict how big this distortion as the Jahn-Teller distortion involves the
t2g set of orbitals, so we can tell which distortion will happen but the effect will not be very big because these orbitals are not pointing directly at the ligands.
Now, when we consider our d
4 system, both compression and elongation successfully remove degeneracy and gain the same amount of stabilisation energy (0.5
δ1).
Therefore, we can conclude that when a Jahn-Teller distortion involves the
eg set of orbitals we know that it will undergo some kind of distortion but we cannot tell which distortion will happen and the effect will usually quite noticeable because these orbitals are pointing directly the ligands. Commonly, a complex compound could only have one distortion even both distortion give the same effect and one way to know which distortion is by using spectroscopy; one of the example is
[Cu(OH2)6]2+ (d
9) has tetragonal elongation although both tetragonal and compression give the same stabilisation.
 |
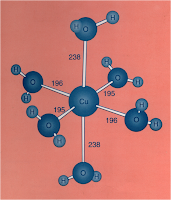| Structure of [Cu(OH2)6]2+ |
From Jahn-Teller distortion, we could explain where the shoulder comes from. The shoulder comes from the electronic transition into different energy level of the distorted complex as shown below.
 |
| Electronic transitions of "shoulder" peak |
Furthermore, Jahn-Teller distortions do occur in tetrahedral complexes, but they usually involve distortions of bond angles rather than bond lengths and are much more difficult to predict.
where E corresponds to ∆o (J mol-1), h is the Planck's constant (6.626 x 10-34 J s), c is the speed of light (approximately 3.00 x 10-34 m s-1), is Avogadro's number (6.022 x 1023 mol-1)and λ is the wavelength of the highest peak (m). However, in the spectrum above, the spectrum has a distinguish characteristic such as the broad peak and the "shoulder, as well a high absorption in the UV region where we will explain it later.
From the splitting above, we no longer have a choice of where to put our electron, so the degeneracy has been successfully removed and the complex have gained 2/3 δ2 of extra stabilisation energy. Now, if we consider the tetragonal elongation we have
and we still have a choice of where to put our electron, so the degeneracy has not been successfully removed and the complex have only gained 1/3 δ2 of extra stabilisation energy. Hence, this distortion does not work so [Ti(OH2)6]3+ could only has tetragonal elongation.
Therefore, we can conclude that when a Jahn-Teller distortion involves the eg set of orbitals we know that it will undergo some kind of distortion but we cannot tell which distortion will happen and the effect will usually quite noticeable because these orbitals are pointing directly the ligands. Commonly, a complex compound could only have one distortion even both distortion give the same effect and one way to know which distortion is by using spectroscopy; one of the example is [Cu(OH2)6]2+ (d9) has tetragonal elongation although both tetragonal and compression give the same stabilisation.
Comments