Entropy: The 2nd and 3rd Laws of Thermodynamics
In this section, we will have a discussion about the origin of spontaneity of process by looking some of the thermodynamics properties, one of it is entropy. Besides that, we will also see the thermodynamics laws that become the foundations of the concept of entropy which are the 2nd and 3rd laws of thermodynamics. Furthermore, we will see one of the application of the 2nd law of thermodynamics in Carnot engine.
In most of the cases, entropy is described as the disorderedness of a system but this definition is not necessarily true. The entropy can be described as the distribution of energy of a system as we can see from an example of the bouncing ball. We can begin to understand the role of the distribution of energy by thinking about a ball (the system) bouncing on a floor (the surroundings). The ball does not rise as high after each bounce because there are inelastic losses in the materials of the ball and floor. The kinetic energy of the ball’s overall motion is spread out into the energy of thermal motion of its particles and those of the floor that it hits. The direction of spontaneous change is towards a state in which the ball is at rest with all its energy dispersed into disorderly thermal motion of molecules in the air and of the atoms of the virtually infinite floor
Early on in the development of thermodynamics, it was believed that if a reaction was exothermic, it was spontaneous. Let consider the following reaction:
The reaction is endothermic, but it is a spontaneous process. Hence, there should be another factor that drives the reaction spontaneously. Before we have a discussion about that factor, let examine the 2nd law of thermodynamics.
Besides that, the 2nd law of thermodynamics states also about entropy where:
The reaction is endothermic but it is spontaneous because entropy is the driving force of this reaction. The changing state from solid to liquid means the energy can be more distributed in liquid states than in solid states which implies the increasing entropy in the system.
Mathematically, entropy can be defined as:
Therefore, for a measurable change between any two states of a system:
so entropy change will depend from the type of process.Besides that, to calculate the difference in entropy between any two states of a system, we find a reversible path between them, and integrate the energy supplied as heat at each stage of the path divided by the temperature at which heating occurs.
The process will change the entropy of the surroundings by:
and this equation can be applied for a reversible or irreversible process.
Entropy is also a state function, so the value of entropy depends only on the initial state and the final state as illustrated below.
Early on, entropy depends on what type of process that accompanies it. The first case is in isothermal processes and this process is when the temperature is constant (ΔT = 0). Since,
so, q = -w (based on the 1st law of thermodynamics) and the entropy in isothermal reversible expansion processes can be calculated as:
The implication of the second law of thermodynamics can be seen in Carnot cycle which can be described as followed. The first step of this process is the gas undergoes an isothermal expansion from A to B, so the entropy can be calculated as:
The second step (B to C) is the gas is in adiabatic cooling and because it is an adiabatic process q = 0, so ΔS = 0. Then, the process is followed by an isothermal compression (C to D) and the entropy can be calculated as:
Lastly, the process is followed by an adiabatic heating that makes the ΔS is 0 because q = 0. From all the processes in Carnot engine, the ΔS total of the engine can be written as:
Therefore, we need to demonstrate that
Furthermore, A general cycle can be divided into small Carnot cycles. The match is exact in the limit of infinitesimally small cycles. Paths cancel in the interior of the collection, and only the perimeter, an increasingly good approximation to the true cycle as the number of cycles increases, survives. Because the entropy change around every individual cycle is zero, the integral of the entropy around the perimeter is zero too.
Early on, we describe that it is impossible to have an engine with 100% efficiency, so the efficiency of a Carnot engine can be defined as the ration of work performed against heat absorbed. Therefore, efficiency can be written as:
Then, according to the 1st law of thermodynamics, efficiency can be written in term of temperature as followed.
In the earlier of this section, we described the entropy for a reversible process as
However, a spontaneous process is an irreversible process, by definition, which that must mean
and this equation is known as Clasius inequality. Then, if the system is isolated, so
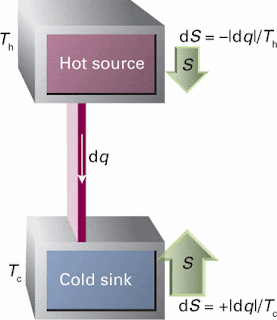
In a Carnot engine, the entropy changes can be seen as: when energy leaves a hot reservoir as heat, the entropy of the reservoir decreases. When the same quantity of energy enters a cooler reservoir, the entropy increases by a larger amount. Hence, overall there is an increase in entropy and the process is spontaneous. Relative changes in entropy are indicated by the sizes of the arrows.
In isothermal reversible expansion, we described the entropy as
so we can write the ΔS of the surrounding as
because the ΔS total of the universe should be 0 in reversible process. Meanwhile, in isothermal irreversible free expansion processes w is 0 because the system expands freely as there is no external pressure against it. Therefore, it implies that q is 0 and ΔS of surrounding is also 0 which means
The phase change as we described in the earlier example, the entropy is one of the driving force of this reaction and the phase change will introduce the entropy change. This process happens at constant and if it is happens at constant pressure, ΔS is
Therefore, from the equation above it can be deduced that an exothermic phase change will decrease the entropy and if it is an endothermic phase change, it will increase the entropy. Furthermore, on the table below is shown some ΔS vaporisation of some compounds.
From the table above, it can be seen that most of the compounds have the entropies of vaporisation around 85 J K-1 mol-1. The anomalous value of water and methane is due to the intermolecular forces as water exhibits hydrogen bonding interaction and methane is relatively the least non-polar molecule. The entropy is also a function of temperature as shown in figure below.
The variation of entropy with temperature at constant pressure can be written as:
then, by factorising in phase transition it can be written as:
From the phase changes, we can say that the motion increases as we progress from solid to liquid and to gas, hence
Then, the total entropy of a system and surroundings will always increase during spontaneous change and the entropy increases as a function of temperature.
Lastly, the third law of thermodynamics states that:
o) and this value is for 25 oC. Because entropy is a state function, the entropy of reaction can be calculated as:
where v is the stoichiometric coefficient and So is the standard entropy of the substance.
 |
| An idealised (impossible) engine |
In most of the cases, entropy is described as the disorderedness of a system but this definition is not necessarily true. The entropy can be described as the distribution of energy of a system as we can see from an example of the bouncing ball. We can begin to understand the role of the distribution of energy by thinking about a ball (the system) bouncing on a floor (the surroundings). The ball does not rise as high after each bounce because there are inelastic losses in the materials of the ball and floor. The kinetic energy of the ball’s overall motion is spread out into the energy of thermal motion of its particles and those of the floor that it hits. The direction of spontaneous change is towards a state in which the ball is at rest with all its energy dispersed into disorderly thermal motion of molecules in the air and of the atoms of the virtually infinite floor
Early on in the development of thermodynamics, it was believed that if a reaction was exothermic, it was spontaneous. Let consider the following reaction:
 |
| William Thomson, 1st Baron Kelvin |
No process is possible in which the sole result is the absorption of heat from a reservoir and its complete conversion into work.This law implies that it is impossible to have a 100% engine efficiency and this statement was formulated by Lord Kelvin. This concept will be brought later for Carnot cycle.
Besides that, the 2nd law of thermodynamics states also about entropy where:
the entropy of an isolated system increases in the course of a spontaneous change.If we return to the reaction below
The reaction is endothermic but it is spontaneous because entropy is the driving force of this reaction. The changing state from solid to liquid means the energy can be more distributed in liquid states than in solid states which implies the increasing entropy in the system.
Mathematically, entropy can be defined as:
Therefore, for a measurable change between any two states of a system:
so entropy change will depend from the type of process.Besides that, to calculate the difference in entropy between any two states of a system, we find a reversible path between them, and integrate the energy supplied as heat at each stage of the path divided by the temperature at which heating occurs.
The process will change the entropy of the surroundings by:
and this equation can be applied for a reversible or irreversible process.
Entropy is also a state function, so the value of entropy depends only on the initial state and the final state as illustrated below.
 |
| Entropy as a state function |
Early on, entropy depends on what type of process that accompanies it. The first case is in isothermal processes and this process is when the temperature is constant (ΔT = 0). Since,
so, q = -w (based on the 1st law of thermodynamics) and the entropy in isothermal reversible expansion processes can be calculated as:
The second step (B to C) is the gas is in adiabatic cooling and because it is an adiabatic process q = 0, so ΔS = 0. Then, the process is followed by an isothermal compression (C to D) and the entropy can be calculated as:
Lastly, the process is followed by an adiabatic heating that makes the ΔS is 0 because q = 0. From all the processes in Carnot engine, the ΔS total of the engine can be written as:
Therefore, we need to demonstrate that
Furthermore, A general cycle can be divided into small Carnot cycles. The match is exact in the limit of infinitesimally small cycles. Paths cancel in the interior of the collection, and only the perimeter, an increasingly good approximation to the true cycle as the number of cycles increases, survives. Because the entropy change around every individual cycle is zero, the integral of the entropy around the perimeter is zero too.
 |
| Carnot cycle |
Early on, we describe that it is impossible to have an engine with 100% efficiency, so the efficiency of a Carnot engine can be defined as the ration of work performed against heat absorbed. Therefore, efficiency can be written as:
Then, according to the 1st law of thermodynamics, efficiency can be written in term of temperature as followed.
In the earlier of this section, we described the entropy for a reversible process as
and this equation is known as Clasius inequality. Then, if the system is isolated, so
dS > 0;
and if the system is not isolatedIn a Carnot engine, the entropy changes can be seen as: when energy leaves a hot reservoir as heat, the entropy of the reservoir decreases. When the same quantity of energy enters a cooler reservoir, the entropy increases by a larger amount. Hence, overall there is an increase in entropy and the process is spontaneous. Relative changes in entropy are indicated by the sizes of the arrows.
In isothermal reversible expansion, we described the entropy as
so we can write the ΔS of the surrounding as
because the ΔS total of the universe should be 0 in reversible process. Meanwhile, in isothermal irreversible free expansion processes w is 0 because the system expands freely as there is no external pressure against it. Therefore, it implies that q is 0 and ΔS of surrounding is also 0 which means
The phase change as we described in the earlier example, the entropy is one of the driving force of this reaction and the phase change will introduce the entropy change. This process happens at constant and if it is happens at constant pressure, ΔS is
Therefore, from the equation above it can be deduced that an exothermic phase change will decrease the entropy and if it is an endothermic phase change, it will increase the entropy. Furthermore, on the table below is shown some ΔS vaporisation of some compounds.
From the table above, it can be seen that most of the compounds have the entropies of vaporisation around 85 J K-1 mol-1. The anomalous value of water and methane is due to the intermolecular forces as water exhibits hydrogen bonding interaction and methane is relatively the least non-polar molecule. The entropy is also a function of temperature as shown in figure below.
 |
| Entropy as a function of temperature |
then, by factorising in phase transition it can be written as:
From the phase changes, we can say that the motion increases as we progress from solid to liquid and to gas, hence
Then, the total entropy of a system and surroundings will always increase during spontaneous change and the entropy increases as a function of temperature.
Lastly, the third law of thermodynamics states that:
All perfect crystalline materials have zero entropy at 0 K;therefore, the 3rd law of thermodynamics defines the standard entropy of a material where it can be written as the absolute standard value of entropy (S
where v is the stoichiometric coefficient and S
























Comments