Fundamentals of Molecular Bonding: Hybridisation and Molecular Orbital Theory
In this section, we will have a discussion about the covalent bonding in a molecule from two point of view, hybridisation and molecular orbital (MO) theory. In this section we will have a discussion about the hybridisation related to some fundamental geometries and in MO theory, we will see how to construct a simple MO for diatomic molecule.
This section is a continuity from previous discussion about VSEPR (see A Quick Guide to VSEPR). From VSEPR calculations help to predict shape of molecules but tell us nothing about the bonding. Once we know the shape of a molecule, we can think about how the atoms are held together, as the nature of bonding, and there is more than one way to do this. The first point of view is the bonding as the localised models, a bond involves overlap of two orbitals on adjacent atoms (hybridisation). In the other hands, the molecular bonding can be seen as delocalised models, a bond involves orbitals spread over the whole molecule (MO theory).
To begin with, we will start our discussion about hybridisation first. The assumption that is used in hybridisation is a bond between two atoms involves overlap between an atomic orbital on the first atom and an atomic orbital on the second. Normally, each of these atomic orbitals contains a single electron and overlap of these two atomic orbitals involves pairing of the electrons.
Then, the big question is raised as why hybridisation is required as VSEPR can predict the geometry of molecule. Let take an example of methane; based on VSEPR rules, methane is tetrahedral and indeed methane is tetrahedral. Then, carbon has a filled valence 2s orbital and two half-filled p-orbitals at 90° to each other. Hence, how can we use these orbitals to make tetrahedral bonds? By hybridisation this question can be answered.
In general, hybridisation means mixing and hybrid orbitals are two or more atomic orbitals (mathematical functions) mixed together and a set of hybrid orbitals may be useful to describe the σ-bonds in a molecule. For your information, hybridisation is a model of molecular bonding NOT a phenomenon when a molecule forms a bond.
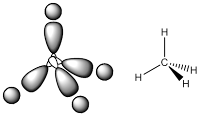
First of our problem is on methane which has tetrahedral geometry and all the atomic orbitals do not have a tetrahedral shape. The first step of hybridisation in methane is the 2s and 2p orbitals of carbon are mixed together to form a degenerate set of orbital and we called sp3 orbital. In sp3 orbital all the orbitals are arranged in tetrahedral arrangement to have minimum repulsion.
As you noticed from the energy level diagram there are 2 dashed line are called correlation line and in hybrid orbital all electron in parallel spin. This arrangement allows the electrons to be paired with another atom. In case of methane, the electrons are paired with 1s orbital of H atom. Besides that, as you observe closely, there is a black dot in the middle of small lobe in hybrid orbital and it is the nucleus. It is a common mistake to put the nucleus between the big and small lobes, but it should be in the small lobe as shown below.
From the sp3 hybrid orbital, we can say that each sp3 hybrid contains 25% s character and 75% p character. Furthermore, if a VSEPR prediction suggests the central atom is tetrahedral then the central atom is sp3 hybridised.
The next hybrid orbital is sp hybridisation which is a mixed between one s and one p orbital to form a linear arrangement, such as BeH2. An sp hybrid orbital contains 50% s character and 50% p character, and if a VSEPR prediction suggests the central atom is linear, so it is an sp hybridised. The energy level diagram is shown below.
Another common hybridised orbital is sp2 hybridisation which is a mixed between one s and two p orbitals to form a trigonal planar arrangement, such as BF3. An hybrid sp2 hybrid orbital contains 33% s character and 67% p character, and if a VSEPR prediction suggests the central atom is trigonal planar, so it is an sp2 hybridised. The energy level diagram of sp2 hybridised orbital is shown below.
Hybridisation is also common to be used to describe the bonding of carbon-based compounds such as alkenes, alkynes, or even allene. Firstly, let take an example of the simplest alkenes which is ethene. Basically, the hybridisation of carbon central atom is sp2, so the energy level diagram is shown below.
From the energy level diagram, we see there is an electron in p-orbital which bonds to another electron in another p-orbital to form π bond as shown by dashed line connecting two lobes. Meanwhile, σ bond is formed from the overlapping of sp2 hybrid orbital. The same overlap scheme also happens in ethyne where in this case 2 p-orbitals form 2 π-bonds as shown below.
In benzene, as all the carbon atoms are sp2 hybridised it makes benzene can form an extended delocalised system within the ring and this delocalisation implies the relatively high stability of benzene.
Another interesting case is in allenes as 2 double bonds are next to each others, so one of the π-bond have to rotate 90° from z-axis into y-axis, or in another words the p-orbital is in orthogonal. The hybridisation scheme of allene is shown below.
Until this far, we only discuss the highest coordination number up to 4 which is a tetrahedral. Hybridisation can also be used to rationalise the bonding in higher coordination number such as 5 and 6, as VSEPR predict the shape is trigonal bipyramidal and octahedral respectively. In table below is shown the state of hybridisation for some coordination numbers up to 6.
As you notice from the table above, there are 2 possible geometries for coordination number of 4 and 5. Coordination number of 4 which exhibits square planar shape commonly happens in transition metal complexes. Meanwhile, the difference in geometry of dsp3 hybridisation is due to the d orbital used in the bonding, trigonal bipyramidal uses dz2 where square-based pyramid geometry uses dx2−y2.
The last part of this section will discuss about another model in bonding which is molecular orbital theory (MO theory). Basically, this model describes the bonding as delocalised models, where the electrons are spread along the bond. The MO theory is used to explain some facts that cannot be explain by simply looking at the lewis structure. For example is O2, which is a paramagnetic molecule and in liquid state has blue colour. From the magnetic properties, it means O2 has unpaired electrons which does not show in Lewis structure. Furthermore, the colour of liquid O2 happens due to electron transitions in energy level of O2.
The basic principle of MO theory is based on the superposition of wave principle as the interactions of 2 wave function of atomic orbitals. As the wave function of atomic orbitals are in the same phase, it forms a constructive superposition (in-phase combination); in the other sides where 2 waves are in the opposite phase it forms a destructive superposition (out-of-phase combination). In term of MO theory where 2 wave functions form a constructive superposition it is called bonding orbital, in the other sides where they form destructive superposition it is called antibonding orbital.
In atoms, electrons are located in atomic orbitals with a variety of shapes and particular energies and each orbital is an equation. In molecules, electrons are located in molecular orbitals with a variety of shapes and particular energies and each orbital is an equation. Conceptually, the hydrogen atom is made up from a proton and an electron. The electron in the H atom is located in an orbital centred on the proton.
The first case of the MO theory is the species of H2+, where it only has 1 electron. The H2+ molecule is made up from two protons and an electron. The electron is located in an orbital centred on the two protons. Instead of being in atomic 1s orbital associated with one nucleus, the electron in H2+ is in a molecular orbital associated with two nuclei. In molecules, the energies of atomic orbitals can be represented on energy level diagrams and aufbau principle are used to populate energy levels with as many electrons as we have for the atom in question. Hence, the MO for H2+ molecule can be drawn as shown below.
Furthermore, if we want to draw the MO for H2 and He2 are shown below.
For the second period of diatomic molecule, Li2 and Be2 are generally the same as H2 and He2, with the only different orbital involved in bonding (2s orbitals instead of 1s). For the p-block elements (B2 to Ne2), there are an addition level as p-orbitals involve. The p-orbitals as we saw in hybridisation gives π and σ bond can be seen as well in MO and for example, we can use our big question which is O2 as the MO is shown below.
As you can see from the MO above, we can definitely see there are 2 unpaired electrons at π* orbitals which causes paramagnetic property of O2. Besides that, we can rationalise the number of bonding that we are familiar from Lewis structure of O2 by calculating the bond order. The bond order can be calculated as:
so from the equation above, the bond order of O2 is:
From the BO calculation, we can see that the BO is the same number of bonds in lewis structure. Furthermore, the BO can be used to predict the bond length of the compounds as higher bond order gives shorter bonds as shown below.
Another interesting case in MO is at B2 to Ne2 where the situation is a little more complex because interactions between σs and σp orbitals. This interactions cause one of the orbitals has lower energy and the other one is higher, so it causes the σp has higher energy than π orbital as shown in C2 molecule.
As you see from the diagram above, the label for σ orbitals are σ1 or σ2, instead of σs or σp as those orbitals are interact with each other. The interaction of those orbitals are allowed because the energy different is not quite big and the important one is both of them have the same symmetry. If we compare C2 molecule with ethene as both of them has bond order of 2. From hybridisation, we can tell that the bonding in ethene is composed of a σ bond and a π bond, but in C2 molecule the bonding is composed of 2 bonds.
MO theory can also be applied for heterodiatomic molecules with the only difference is both atom has different energy level which means the energy level diagrams will be asymmetric. For example, CO has the same total number of electrons as N2, so we can assume the MO of CO is almost similar with N2. However, as C is less electronegative than O, the atomic energy level of C is higher than O as the electron in O is more stabilised than C due to higher nuclear charge. Thus, the MO of CO is shown below.
Another case is HF as the F energy levels are all below that of H, so there is no overlap between 2 of the F p-orbitals and the H s-orbital. The reason of no overlap between those 2 orbitals is due to different symmetry and 2s orbital of is too low to interact with H 1s orbital. Thus, the MO of HF is shown below.
The σ* orbital is largely an atomic hydrogen 1s orbital and the σ-bonding orbital is largely a fluorine 2pz orbital. In effect, there is considerable transfer of electron density from H atom to F atom. This result in a charge imbalance in the molecule, with H end somewhat positive and the F end somewhat negative.
This section is a continuity from previous discussion about VSEPR (see A Quick Guide to VSEPR). From VSEPR calculations help to predict shape of molecules but tell us nothing about the bonding. Once we know the shape of a molecule, we can think about how the atoms are held together, as the nature of bonding, and there is more than one way to do this. The first point of view is the bonding as the localised models, a bond involves overlap of two orbitals on adjacent atoms (hybridisation). In the other hands, the molecular bonding can be seen as delocalised models, a bond involves orbitals spread over the whole molecule (MO theory).
To begin with, we will start our discussion about hybridisation first. The assumption that is used in hybridisation is a bond between two atoms involves overlap between an atomic orbital on the first atom and an atomic orbital on the second. Normally, each of these atomic orbitals contains a single electron and overlap of these two atomic orbitals involves pairing of the electrons.
 |
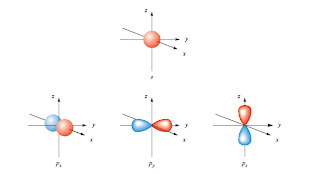| 1s and 2p orbitals |
In general, hybridisation means mixing and hybrid orbitals are two or more atomic orbitals (mathematical functions) mixed together and a set of hybrid orbitals may be useful to describe the σ-bonds in a molecule. For your information, hybridisation is a model of molecular bonding NOT a phenomenon when a molecule forms a bond.
 |
| sp3 hybridisation |
As you noticed from the energy level diagram there are 2 dashed line are called correlation line and in hybrid orbital all electron in parallel spin. This arrangement allows the electrons to be paired with another atom. In case of methane, the electrons are paired with 1s orbital of H atom. Besides that, as you observe closely, there is a black dot in the middle of small lobe in hybrid orbital and it is the nucleus. It is a common mistake to put the nucleus between the big and small lobes, but it should be in the small lobe as shown below.
 |
| The nucleus position in hybridised orbital |
From the sp3 hybrid orbital, we can say that each sp3 hybrid contains 25% s character and 75% p character. Furthermore, if a VSEPR prediction suggests the central atom is tetrahedral then the central atom is sp3 hybridised.
The next hybrid orbital is sp hybridisation which is a mixed between one s and one p orbital to form a linear arrangement, such as BeH2. An sp hybrid orbital contains 50% s character and 50% p character, and if a VSEPR prediction suggests the central atom is linear, so it is an sp hybridised. The energy level diagram is shown below.
 |
| sp hybridisation |
Another common hybridised orbital is sp2 hybridisation which is a mixed between one s and two p orbitals to form a trigonal planar arrangement, such as BF3. An hybrid sp2 hybrid orbital contains 33% s character and 67% p character, and if a VSEPR prediction suggests the central atom is trigonal planar, so it is an sp2 hybridised. The energy level diagram of sp2 hybridised orbital is shown below.
 |
| sp2 hybridisation |
Hybridisation is also common to be used to describe the bonding of carbon-based compounds such as alkenes, alkynes, or even allene. Firstly, let take an example of the simplest alkenes which is ethene. Basically, the hybridisation of carbon central atom is sp2, so the energy level diagram is shown below.
 |
| Ethene hybridisation |
 |
| Ethyne hybridisation |
 |
| Benzene |
 |
| Allene |
The last part of this section will discuss about another model in bonding which is molecular orbital theory (MO theory). Basically, this model describes the bonding as delocalised models, where the electrons are spread along the bond. The MO theory is used to explain some facts that cannot be explain by simply looking at the lewis structure. For example is O2, which is a paramagnetic molecule and in liquid state has blue colour. From the magnetic properties, it means O2 has unpaired electrons which does not show in Lewis structure. Furthermore, the colour of liquid O2 happens due to electron transitions in energy level of O2.
The basic principle of MO theory is based on the superposition of wave principle as the interactions of 2 wave function of atomic orbitals. As the wave function of atomic orbitals are in the same phase, it forms a constructive superposition (in-phase combination); in the other sides where 2 waves are in the opposite phase it forms a destructive superposition (out-of-phase combination). In term of MO theory where 2 wave functions form a constructive superposition it is called bonding orbital, in the other sides where they form destructive superposition it is called antibonding orbital.
In atoms, electrons are located in atomic orbitals with a variety of shapes and particular energies and each orbital is an equation. In molecules, electrons are located in molecular orbitals with a variety of shapes and particular energies and each orbital is an equation. Conceptually, the hydrogen atom is made up from a proton and an electron. The electron in the H atom is located in an orbital centred on the proton.
The first case of the MO theory is the species of H2+, where it only has 1 electron. The H2+ molecule is made up from two protons and an electron. The electron is located in an orbital centred on the two protons. Instead of being in atomic 1s orbital associated with one nucleus, the electron in H2+ is in a molecular orbital associated with two nuclei. In molecules, the energies of atomic orbitals can be represented on energy level diagrams and aufbau principle are used to populate energy levels with as many electrons as we have for the atom in question. Hence, the MO for H2+ molecule can be drawn as shown below.
 |
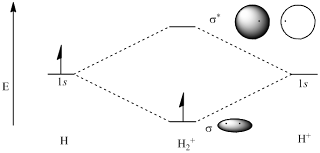| The MO for H2+ |
 |
| The MO for H2 and He2 |
For the second period of diatomic molecule, Li2 and Be2 are generally the same as H2 and He2, with the only different orbital involved in bonding (2s orbitals instead of 1s). For the p-block elements (B2 to Ne2), there are an addition level as p-orbitals involve. The p-orbitals as we saw in hybridisation gives π and σ bond can be seen as well in MO and for example, we can use our big question which is O2 as the MO is shown below.
 |
| The MO for O2 |
Another interesting case in MO is at B2 to Ne2 where the situation is a little more complex because interactions between σs and σp orbitals. This interactions cause one of the orbitals has lower energy and the other one is higher, so it causes the σp has higher energy than π orbital as shown in C2 molecule.
 |
| The MO for C2 |
MO theory can also be applied for heterodiatomic molecules with the only difference is both atom has different energy level which means the energy level diagrams will be asymmetric. For example, CO has the same total number of electrons as N2, so we can assume the MO of CO is almost similar with N2. However, as C is less electronegative than O, the atomic energy level of C is higher than O as the electron in O is more stabilised than C due to higher nuclear charge. Thus, the MO of CO is shown below.
 |
| The MO for CO |
Another case is HF as the F energy levels are all below that of H, so there is no overlap between 2 of the F p-orbitals and the H s-orbital. The reason of no overlap between those 2 orbitals is due to different symmetry and 2s orbital of is too low to interact with H 1s orbital. Thus, the MO of HF is shown below.
 |
| The MO for HF |
Comments