In this section we will see the solid structure of metals and their ionic compounds of
s- and
p- block elements. Besides that, we will also see the lattice enthalpy and the enthalpy of dissolution of ionic compounds, as well their periodic trends.
Solid State Structures of Metals
In general, the metallic elements would arrange itself in metallic lattice in the most efficient was in a fixed volumes. Then, it is assume that atoms as hard spheres and all atoms have identical size. From those assumption, there are 4 main solid state structures of metals; cubic close packed (CCP), hexagonal close packed (HCP), simple cubic, and body-centred cubic. The elements will arrange in certain crystal lattice depends on its atomic (metallic) radius, and most of metals are CCP or HCP.
 |
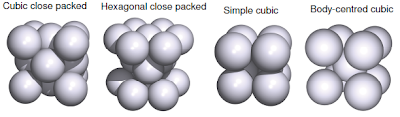| Metallic solid structures |
The structure of solid compound or element can be determined from X-ray crystallography, where X-rays diffracted at angles dependent on arrangement of atoms in crystal structure. Now, the problem is what is the most efficient way packing arrangement.
 |
| X-ray crystallography |
Firstly, a single close-packed layer is formed where each atom in contact with 6 others in that layer, this is called hexagonal arrangement. The second layer is put above holes holes in 1st layer, so only 50% of the holes are covered. Now, when the 3rd layer is going to be placed, there are 2 possible position. The first possibility is to place the 3rd layer above atoms in 1st layer to form ABAB sequence, or the 3rd layer is placed above uncovered holes in 1st layer to form ABCA sequence (the 4th layer will be placed above atoms in first layer).
 |
| The close-packed arrangements |
Therefore, atoms in both sequences have coordination number of 12, and for ABAB sequence will form HCP arrangement and ABCA sequence form CCP arrangement. Moreover, most of metals adopt these structures.
 |
HCP (left), space filling diagram of CCP or FCC (centre),
the positions of atom centres in CCP (right) |
In CCP structures only 74% of space is occupied, so there are 2 types of cavities in CCP, tetrahedral holes and octahedral holes. A tetrahedral holes is where an atom placed over a hole in the layer below creates a cavity surrounded tetrahedrally by four atoms and the number of tetrahedral holes is double the number of atoms. Meanwhile, octahedral holes is when a hole in one layer lies directly above a hole in the layer below, a cavity surrounded octahedrally by six atoms is created and the number of octahedral holes is equal to the number of atoms.
 |
| Tetrahedral hole (left) and octahedral hole (right) |
 |
| CCP or FCC |
A crystal lattice is formed from unit cells stacked together, so a unit cell is the smallest repeating unit in a crystal structure. The next problem is how to count the atoms (or ions) in a cubic unit cell. There are some guidances how to count the atoms as shown below.
- An atom completely contained within the cube belongs only to that cell and counts as 1
- An atom at the centre of a face of the cube is shared by two cells and counts as 1/2
- An atom at an edge of the cube is shared by four cells and counts as 1/4
- An atom at a corner of the cube is shared by eight cells and counts as 1/8
Therefore, in CCP unit cells there are 4 atoms (6x1/2 + 8x1/8). Moreover, for BCC and simple cube are shown on figure below.
The periodic trends of metallic structures in group 1 elements are BCC with decreasing melting point as down the group and in group 2 is a mixture of HCP (Be and Mg), CCP (Ca and Sr), and BCC (Ba and Ra). Moreover, smaller atomic radius prefer a close-packed structure.
Structures of Ionic Crystal Lattices and the Enthalpy of Hydration
In
s- and
p- block ionic compounds mainly form 2 types of ionic lattice structure, the NaCl (rock salt) structure and the CsCl structure. The rock salt structure can be considered as a FCC array of chloride ions with sodium ions in octahedral holes. Therefore, each ion has coordination number of 6 and the unit cell is comprised of 4 sodium ions and 4 chloride ions. Moreover, larger cations (radius ratio of cation and anion > 0.73) will not fit in the octahedral holes.
 |
| Ionic crystal structures of NaCl and CsCl |
In the CsCl structure, a simple cubic array of chloride ions with caesium ions at centres of cubes (or vice versa). Moreover, another ionic compounds of
s- and
p- block elements can have another types of ionic crystal lattice.
 |
| Born-Haber cycle |
The stability of ionic compounds can be predicted by looking its lattice enthalpy. Lattice enthalpy is the enthalpy change that accompanies formation of one mole of a solid compound in its usual lattice structure from its constituent gaseous ions. Moreover, there are 2 ways to calculate lattice enthalpy of an ionic compound, Born-Haber cycle and Born-Lande Equation. Moreover, Born-Haber cycle is based on the Hess's law and for example we will see the lattice enthalpy of NaCl.
The other way is by using Born-Lande Equation which is based on Coulomb's Law, and the Born-Lande Equation is shown below.
There are 2 interesting constant at the equation which are
M (Madelung constant) and
n (Born exponent). Madelung constant is come from as the lattice enthalpy is the energy that is released when the ions from the infinite distance close together to form ionic crystal, so the interaction between all ions must be taken into calculation. For example in NaCl crystal and as the 0 marker is the sodium ion in the centre of unit cell. There are 6 chloride ions at a distance
r, 12 sodium ions at a distance
r√2, 8 chloride ions at a distance of
r√3, 6 sodium ions at a distance of 2
r, and so on until infinite. Then, by substituting that statements into Coulomb's law, we will see a series in the equation.
The series of terms converges to a simple value which is the Madelung constant and Madelung constant only depends on the geometric of structure of the crystal lattice. It does not depend on the type of ions. Meanwhile,
n (Born exponent) takes into account repulsion between electron clouds of the ions at short distance.
When we compare those methods, we might see some discrepancy of the lattice enthalpy as shown on table below.
This deviation is caused by in Born-Lande equation only takes into calculation the electrostatic interaction between ions, meanwhile in this case a high charge density of ions can distort large ion to induce some covalent character that makes the discrepancy. Therefore, largest deviations happens for small cations with large polarisable anions leading to some covalency. The periodic trend of lattice enthalpy based on Born-Lande equation is the lattice enthalpy becomes less exothermic as increases the radius (
r) and becomes more exothermic as the the charge increases. Hence, a compound will have a highly exothermic lattice enthalphy when it has small and highly charged ions, which means the ionic compound is more stable.
The ionic compound is soluble in water and the solubility of the ions can be seen from the enthalpy of hydration. The enthalpy of hydration is the enthalpy change when a gas phase ion is solvated in aqueous solution. Moreover, small and more highly charged ions are more strongly hydrated, which means the enthaly of hydration becomes more exothermic.
After that, the solubility of ionic compound can be determined from its enthalpy of hydration, and it can be calculated from the Hess's law from the lattice enthalpy and the hydration enthalphies of the cation and anion. Then, salts with ions of widely different size tend to be the most soluble as the salts with ions of similar size tend to be less soluble. For example, the enthalpy of dissolution of CsF and CsI. We can determine just from the from the lattice enthalpy and the hydration enthalphy of fluoride and iodide ions, since both of them are caesium salts. Large hydration enthalpy of fluoride (due to small and higly charged anion) means that CsF is more soluble than CsI, despite stronger lattice enthalpy fro CsF.
The periodic trends of metallic structures in group 1 elements are BCC with decreasing melting point as down the group and in group 2 is a mixture of HCP (Be and Mg), CCP (Ca and Sr), and BCC (Ba and Ra). Moreover, smaller atomic radius prefer a close-packed structure.
There are 2 interesting constant at the equation which are M (Madelung constant) and n (Born exponent). Madelung constant is come from as the lattice enthalpy is the energy that is released when the ions from the infinite distance close together to form ionic crystal, so the interaction between all ions must be taken into calculation. For example in NaCl crystal and as the 0 marker is the sodium ion in the centre of unit cell. There are 6 chloride ions at a distance r, 12 sodium ions at a distance r√2, 8 chloride ions at a distance of r√3, 6 sodium ions at a distance of 2r, and so on until infinite. Then, by substituting that statements into Coulomb's law, we will see a series in the equation.
The series of terms converges to a simple value which is the Madelung constant and Madelung constant only depends on the geometric of structure of the crystal lattice. It does not depend on the type of ions. Meanwhile, n (Born exponent) takes into account repulsion between electron clouds of the ions at short distance.
This deviation is caused by in Born-Lande equation only takes into calculation the electrostatic interaction between ions, meanwhile in this case a high charge density of ions can distort large ion to induce some covalent character that makes the discrepancy. Therefore, largest deviations happens for small cations with large polarisable anions leading to some covalency. The periodic trend of lattice enthalpy based on Born-Lande equation is the lattice enthalpy becomes less exothermic as increases the radius (r) and becomes more exothermic as the the charge increases. Hence, a compound will have a highly exothermic lattice enthalphy when it has small and highly charged ions, which means the ionic compound is more stable.
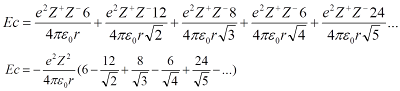
Comments