Atoms and the Periodic Table II: Quantisation of Energy

As it was discussed previously (Atom and Periodic Table: Wave Properties), we have seen a properties of electromagnetic radiation that is emitted from an atom as wavelength and as well a glimpse of its particle properties. In this section, we will discuss about its particle properties more thoroughly, especially related with energy, and about hydrogenic atom spectrum. In this section and later on, we will discuss about this matter by using H atom, because H atom is the simplest atomic system in the periodic table (1 electron system).


The energy that released from radiated atom is in the form of electromagnetic radiation. Moreover, electromagnetic radiation carries energy in the form as package, and it is known as quantised energy. The relationship between energy and wavelength as we have shown in Atom and Periodic Table: Wave Properties is:

Therefore, every wavelength carries different energy and as the wavelength decreases, energy increases. This equation is different as classical mechanics says. In classical mechanics, the energy of atom in similar way as the "hill" of energy (continuous), whether in quantum mechanics is shown as a "ladder" or commonly known as energy level.

http://dev.physicslab.org/img/e8c5c99d-38fd-42cf-bc03-0f6b819c5eed.gif

As a result of the energy "ladder" in atomic structure, it would give a line spectrum. The spectroscopy basically works as in the equation below shown for H sample.

A sample of hydrogen gas undergoes a reaction in highly electric discharge to form an excited state of H atom (H*). In this excited state, the electron of hydrogen atom is promoted to higher energy level. After that, H* is back to the ground state (H) and it releases photon energy and this photon energy will be shown as emission spectrum or line spectra. The line spectra basically is a list of emitted a certain frequency or wavenumber.

https://www.e-education.psu.edu/astro801/files/astro801/image/electron_energy_levels_KL.jpg

Therefore, from this observation there are 3 questions appear about this phenomenon. Firstly is why this can happen. As we have discussed before, this line spectra is agree with the theory that atom consists as energy level, not as continuous energy. 

Second question is a formula should be made to predict this behaviour. At the beginning, a Swiss mathematician and physicist, Johann J. Balmer, tried to formulate this behaviour. He had a series of line spectra: 364.5 nm (UV), 410.2 nm (UV), 434.1 nm (violet), 486.1 nm (red), and 656.3 nm (blue); and he came up with a formula:

After that, not only Balmer that came up with that equation, there were another 5 scientists that came up with another series. The five scientists are Lyman, Paschen, Brackett, Pfund, and Humphreys. Therefore, a general formula that can predict all the line for H atom is:

 

and for Lyman (n=1), Balmer (n=2), Paschen (n=3), Brackett (n=4), Pfund (n=5), and Humphreys (n=6).

Thirdly, from the spectra what does it mean about hydrogen atom. As we see in the equation, each series has a fix value of n and n' (n + 1 up to ∞). As n' is going to ∞, 1/n' is going to 0, so when an electron is promoted up to an ∞ energy level (out from the atom) the wavenumber is simply:

Moreover, for the same formula can be applied from hydrogen-like (hydrogenic) atom. However the different is constant of R which shown as below:

 

When it is applied for hydrogen atom the value of R_X if Z = 1 (1.097 37 x 10⁷ m^-1) is not exactly as R_H (1.096 77 x 10⁷ m^-1). This different is basically caused in Bohr model it is assumed that the electron is orbiting the nucleus, but it is actually both nucleus and electron are orbiting a centre of mass. Since the nucleus (proton) has mass almost 2000 times mass of electron, so the centre of mass is almost 1/2000 of distance between nucleus and electron. Then, from the reduced mass, the system of proton and electron are turned into an object that have mass orbiting a centre of mass, and the mass will be turned into reduced mass. The reduced mass is calculated as:

Since mass of proton is almost 2000 times than electron, so the equation can be simplified into:

For hydrogenic atom such as He²⁺, Li³⁺; as the number of proton increases the reduced mass is closer to the mass of electron and the limit will be the mass of electron.

If we back to our Rydberg's general formula, inside the H atom has discrete energies that is counted by an integers (E₁, E₂, E₃, …., E_n). Then, since electron is attracted to proton therefore the energy is:

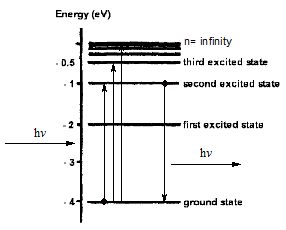
The minus sign indicate the attraction between electron and proton. In the other sides, if there is no minus sign, it means there is no interaction between electron and proton, so electron will easily escape from an atom and we will exist in the form of hot cloud. If we back to the electronic transition process as shown in figure below.

Firstly, if we see the excitation process, when an electron is radiated, it can be promoted into higher energy level. If it is excited into ∞ energy level, we can calculate the required energy as:

The value of energy from the equation above is the ionisation energy for hydrogen atom (13.6 eV).

Secondly, when the electron returns to the ground state, it releases energy in the form of photon. By applying the law of conservation energy we can prove the Rydberg's equation.

Since, E is inversly proportional to n², so the equation become:

Where k is a constant which is R_H.