A Quick Guide to VSEPR
In this section, we will discuss about how to predict geometry of a molecule by using valence shell electron pair repulsion (VSEPR) theory. In this section, we will use this simple method not only to rationalise shape of molecules but we can also predict the geometry of molecules. This method works as well for organic and inorganic structures.
The first thing we need to know about this method is the assumption that is used. The assumptions is atoms in a molecule are bound together by electron pairs called bonding pairs and bonds are usually shared-electron (one from each of the two connected atoms). Some atoms in a molecule may possess pairs of electrons not involved in bonding; these are lone pairs or non-bonded pairs. Electron pairs are negatively charged and will get as far apart from each other as possible. They adopt in which their mutual interactions (repulsion) are minimised. In picture below is shown some preferred geometries and each blue circle represents an electron pair, either a bond pair or a lone pair.
The next step is how to do the VSEPR calculation to predict the geometry of molecules. Lewis dot-and-cross structures are used to represent the bond and a single lewis (dot-and-cross) bond is known as σ-bond. The idea of VSEPR calculation is to calculate the number of vertices associated with the atom of interest (the central atom) in the molecule and each vertex of the coordination polyhedron corresponds to either a σ-bond or a lone pair. Therefore, if we calculate the number of electrons in σ-bonds, we can determine the number of vertices and so determine the shape.
Then, we can assigned the calculation.
Cental atom: C
Valence electron (VE) atom: 4
4 H each provide 1 electron: 4
Total: 8 electrons
divide by 2 to give pairs: 4 electron pairs
4 electron pairs: tetrahderal geometry
4 bond pairs: so 0 lone pairs
Shape: tetrahedral
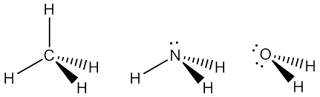
Therefore, we can redraw the lewis structure of CH4 with the shape of tetrahedral and the angle H-C-H in tetrahedral is 109° 28'. As you notice from the picture below, one C-H bond has wedge line which means it is out of the plane and the another C-H bond that is drawn with dashed line represents into the plane.
The determination of a molecule's geometry requires a calculation of the number of electrons contained in the σ orbitals. This number is made up from:
Lewis structure of NH3 and the calculation:
Central atom: N
VE on central atom: 5
3 H each provide 1 electron: 3
Total: 8 electrons
divide by 2 to give pairs: 4 electron pairs
4 electron pairs: tetrahedral geometry
3 bond pairs: so 1 lone pair
shape: pyramidal
Hence, we can redraw the lewis structure of NH3 with the shape of pyramidal and the angle H-N-H in tetrahedral is 106.6°. As you notice, the angle H-N-H is smaller than H-C-H is due to lone pair electron repulsion which requires more space than electron-bonding pair.
Central atom: O
VE on central atom: 6
2 H each provide 1 electron: 2
Total: 8 electrons
divide by 2 to give pairs: 4 electron pairs
4 electron pairs: tetrahedral geometry
2 bond pairs: so 2 lone pairs
Shape: bent or V-shape
By redrawing the geometry of water, we can see the angle of H-O-H bond is much smaller (104.5°) than H-N-H and H-C-H bond due to more electron-lone pairs.
Central atom: B
VE on central atom: 3
3 F each provide 1 electron: 3
Total: 6 electrons
divide by 2 to give pairs: 3 electron pairs
3 electron pairs: trigonal geometry
3 bond pairs: so 0 lone pairs
shape: trigonal
The first three examples that we had early on was octet molecules, and now we have a non-octet compound which has 6 valence electron pairs. From this VSEPR calculation we predict the shape as trigonal and the bond angle F-B-F is 120°, which is bigger than tetrahedral compound. Besides that, the expanded octet compounds can also be predicted the geometry of its molecule. For example, compounds that have 5 bonding pairs would form trigonal bipyramidal geometry, as compounds that have 6 bonding pairs would prefer octahedral geometry.
Moreover, in trigonal bipyramidal has 2 bonding positions which are equatorial and axial, but in octahedral all position are equivalent.
VSEPR can also predict the geometry of a charged species and any charge is always localised formally on the central atom, even we know the charge is not on the central atom. In our calculation, the number of positive charges is subtracted from the number of valence electrons on the central atom. In the other sides, the number of negative charges is added to the number of valence electrons on the central atom.
central atom: P
VE on central atom: 5
6 F each provide 1 electron: 6
Add 1 for negative charge: 1
Total: 12 electrons
divide by 2 to give pairs: 6 electron pairs
6 electron pairs: octahedral geometry
6 bond pairs: so 0 lone pairs
Shape: octahedral
From the VSEPR we can predict that every molecule that has 6 electron pairs would have octahedral geometry and F-P-F angle in octahedral is 90°.
central atom: As
VE on central atom: 5
4 Ph each provide 1 electron: 4
subtract 1 for positive charge: -1
Total: 8 electrons
divide by 2 to give pairs: 4 electron pairs
4 electron pairs: tetrahedral geometry
4 bond pairs: so 0 lone pairs
Shape: tetrahedral
Hence, we can we redraw as tetrahedral.
As we already considered the effect on charged molecule, the effect of multiple bond should be considered. Depending upon the element, lewis dot structures allow single, double, and triple bonds but double and triple bonds still only occupy one coordination vertex. Therefore, a single vertex may have 2, 4, or 6 associated electrons. In a lewis single bond is always regarded as σ bond and a lewis double bond is always regarded as a σ and π bond interaction. Moreover, a lewis triple bond is always regarded as a σ + π + π bond interaction.
In VSEPR case let take an example of a double which consist of a σ-bond and a π-bond, so each bond is treated as having one electron from each atom. As are only interested in determining the number of electrons in the σ-framework, so we need to discount the π-electrons. This shows as a -1 for each π-bond in the calculation.
Central atom: C
VE on central atom: 4
1 H providess 1 electron: 1
1 Me provides 1 electron: 1
1 CH2 provides 1 electron: 1
Subtract 1 for π electron: -1
Total: 6 electrons
divide by 2 to give pairs: 3 electron pairs
3 electron pairs: trigonal geometry
3 bond pairs: so 0 lone pairs
Shape: trigonal
Hence we can redraw it as trigonal molecule; moreover the angle Me-C-H is pushed to slightly smaller than 120° due to double bond C=CH2.
central atom: S
VE on central atom: 6
3 F each provide 1 electron: 3
1 N provides 1 electron: 1
Subtract 2 for 2 π electrons: -2
Total: 8 electrons
divide by 2 to give pairs: 4 electron pairs
4 electron pairs: tetrahedral geometry
4 bond pairs: so 0 lone pairs
shape: tetrahedral.
Therefore, we need to draw the structure SF3N with its proper geometry as shown above and the angle F-S-F is slightly smaller than 109.5° due to triple bond S and N.
Another assumptions that we also need to use in our VSEPR that is about space requirement. In VSEPR calculation we assume that lone pairs occupy more space than bonding in electron pairs and double bonds occupy more space than single bonds.
central atom: Cl
VE on central atom: 7
4 O each provide 1 electron: 4
Subtract 4 for 4 π electrons: -4
Add 1 for negative charge: 1
Total: 8 electrons
divide by 2 to give pairs: 4 electron pairs
4 electron pairs: tetrahedral geometry
4 bond pairs: so 0 lone pairs
shape: tetrahedral.
Therefore, we can redraw [ClO4]− as tetrahedral below.
Note: all Cl-O bonds are double bonds (Cl=O bonds).
central atom: Cl
VE on central atom: 7
3 F each provide 1 electron: 3
Total: 10 electrons
divide by 2 to give pairs: 5 electron pairs
5 electron pairs: trigonal bipyramidal geometry
3 bond pairs: so 2 lone pairs
In this case, the shape of ClF3 need a little bit consideration about the positions for lone pairs. From the calculation, it indicates a trigonal bipyramidal structure with three bonding pairs and two lone pairs, so the big question is where to place the lone pairs. There are three possibilities to put two lone pairs in this molecule as shown below.
The first thing we need to consider is lone pairs occupy more angular space and are located closer to their atoms than bond pairs. Hence, the interactions between two lone pairs at any given angle are greater than the interactions between two bonding pairs. The interaction between a lone pair and a bonding pair is somewhere in between. Any given structure will adopt a configuration in which interactions between electron pairs are minimised. To determine the geometry of ClF3, let tabulate those there structures based on the angle.
Note: bp = bonding pair and lp = lone pair
The first step to determine the geometry of ClF3 is to ignore all interactions at angles greater than 90° then cancelling 3 bp-lp as all the structure has 3 bp-lp. Hence, we have our new table as follow.
From table above, we can see when 2 lone pairs are place at equatorial it does not contain lp-lp interaction, so we can deduce that ClF3 has structure T-shaped with 2 equatorial lone pairs as shown below.
Furthermore, by using a similar argument we can show that in all trigonal bipyramidal cases, electron pairs are best placed in equatorial positions (try to predict the geometry of I3− ).
central atom: N
VE on central atom: 5
2 O provide 2 electron: 2
Subtract 2 for 2 π electrons: -2
Total: 5 electrons
divide 2 to give pairs: 2.5 electron pairs
"3" electron pairs: trigonal geometry
2 bond pairs: so "1" lone pair
Shape: bent
For NO2 there is an integral number of electrons but a non-integral number of electron pairs as 2.5 electron pairs must be placed into three orbitals. Hence, the "lone pair" orbital is only "half filled", the O-N-O angle opens (to 134.1°) from the ideal angle of 120°.
Until this far, we only encounter the geometry up to 6 electron pairs, but molecules can have higher electron pairs such as 7 electron pairs which has two possible geometries. The first possible is undistorted pentagonal bipyramidal and the example is IF7. The other possibility is monocapped octahedron, such as XeF6 which 6 bonding pairs and 1 one lone pair. Distorted octahedron sometimes described as monocapped octahedron (lone pair in the capping position).
Furthermore, with higher coordination number the situation is more complex. For instance, the idealised geometry for eight electron pairs (epitomised by the anion [XeF8]2-) is a square antiprism but the energy of other coordination geometries may be similar or more stable in particular cases.
As a conclusion, if you want to have a practice with VSEPR calculation you may visit http://winter.group.shef.ac.uk/chemputer/vsepr.html and for the list of the VSEPR geometry you may visit Valence Shell Electron Pair Repulsion Theory page.
The first thing we need to know about this method is the assumption that is used. The assumptions is atoms in a molecule are bound together by electron pairs called bonding pairs and bonds are usually shared-electron (one from each of the two connected atoms). Some atoms in a molecule may possess pairs of electrons not involved in bonding; these are lone pairs or non-bonded pairs. Electron pairs are negatively charged and will get as far apart from each other as possible. They adopt in which their mutual interactions (repulsion) are minimised. In picture below is shown some preferred geometries and each blue circle represents an electron pair, either a bond pair or a lone pair.
The next step is how to do the VSEPR calculation to predict the geometry of molecules. Lewis dot-and-cross structures are used to represent the bond and a single lewis (dot-and-cross) bond is known as σ-bond. The idea of VSEPR calculation is to calculate the number of vertices associated with the atom of interest (the central atom) in the molecule and each vertex of the coordination polyhedron corresponds to either a σ-bond or a lone pair. Therefore, if we calculate the number of electrons in σ-bonds, we can determine the number of vertices and so determine the shape.
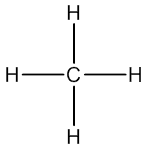
Example 1. Methane (CH4)
The first step is to draw lewis structure of CH4, this step is not necessary to draw the exact geometry as we will predict it later. The lewis structure of is CH4 shown below.Then, we can assigned the calculation.
Cental atom: C
Valence electron (VE) atom: 4
4 H each provide 1 electron: 4
Total: 8 electrons
divide by 2 to give pairs: 4 electron pairs
4 electron pairs: tetrahderal geometry
4 bond pairs: so 0 lone pairs
Shape: tetrahedral
Therefore, we can redraw the lewis structure of CH4 with the shape of tetrahedral and the angle H-C-H in tetrahedral is 109° 28'. As you notice from the picture below, one C-H bond has wedge line which means it is out of the plane and the another C-H bond that is drawn with dashed line represents into the plane.
The determination of a molecule's geometry requires a calculation of the number of electrons contained in the σ orbitals. This number is made up from:
- valence electrons for the atoms is question
- contributions from attached atoms
- contributions from charges (positive or negative)
- contribution to take into account multiple bonds
Example 2. Ammonia (NH3)
Central atom: N
VE on central atom: 5
3 H each provide 1 electron: 3
Total: 8 electrons
divide by 2 to give pairs: 4 electron pairs
4 electron pairs: tetrahedral geometry
3 bond pairs: so 1 lone pair
shape: pyramidal
Example 3. Water (OH2)
Lewis structure of OH2 and the calculation:VE on central atom: 6
2 H each provide 1 electron: 2
Total: 8 electrons
divide by 2 to give pairs: 4 electron pairs
4 electron pairs: tetrahedral geometry
2 bond pairs: so 2 lone pairs
Shape: bent or V-shape
Example 4. BF3
Lewis structure of and the calculation:VE on central atom: 3
3 F each provide 1 electron: 3
Total: 6 electrons
divide by 2 to give pairs: 3 electron pairs
3 electron pairs: trigonal geometry
3 bond pairs: so 0 lone pairs
shape: trigonal
The first three examples that we had early on was octet molecules, and now we have a non-octet compound which has 6 valence electron pairs. From this VSEPR calculation we predict the shape as trigonal and the bond angle F-B-F is 120°, which is bigger than tetrahedral compound. Besides that, the expanded octet compounds can also be predicted the geometry of its molecule. For example, compounds that have 5 bonding pairs would form trigonal bipyramidal geometry, as compounds that have 6 bonding pairs would prefer octahedral geometry.
VSEPR can also predict the geometry of a charged species and any charge is always localised formally on the central atom, even we know the charge is not on the central atom. In our calculation, the number of positive charges is subtracted from the number of valence electrons on the central atom. In the other sides, the number of negative charges is added to the number of valence electrons on the central atom.
Example 5. [PF6]−
lewis structure of [PF6]− and the calculation:VE on central atom: 5
6 F each provide 1 electron: 6
Add 1 for negative charge: 1
Total: 12 electrons
divide by 2 to give pairs: 6 electron pairs
6 electron pairs: octahedral geometry
6 bond pairs: so 0 lone pairs
Shape: octahedral
From the VSEPR we can predict that every molecule that has 6 electron pairs would have octahedral geometry and F-P-F angle in octahedral is 90°.
Example 6. [AsPh4]+
lewis structure of [AsPh4]+ and the calculation:VE on central atom: 5
4 Ph each provide 1 electron: 4
subtract 1 for positive charge: -1
Total: 8 electrons
divide by 2 to give pairs: 4 electron pairs
4 electron pairs: tetrahedral geometry
4 bond pairs: so 0 lone pairs
Shape: tetrahedral
Hence, we can we redraw as tetrahedral.
As we already considered the effect on charged molecule, the effect of multiple bond should be considered. Depending upon the element, lewis dot structures allow single, double, and triple bonds but double and triple bonds still only occupy one coordination vertex. Therefore, a single vertex may have 2, 4, or 6 associated electrons. In a lewis single bond is always regarded as σ bond and a lewis double bond is always regarded as a σ and π bond interaction. Moreover, a lewis triple bond is always regarded as a σ + π + π bond interaction.
In VSEPR case let take an example of a double which consist of a σ-bond and a π-bond, so each bond is treated as having one electron from each atom. As are only interested in determining the number of electrons in the σ-framework, so we need to discount the π-electrons. This shows as a -1 for each π-bond in the calculation.
Example 7. CH2=CHMe
Lewis structure of CH2=CHMe and calculation:VE on central atom: 4
1 H providess 1 electron: 1
1 Me provides 1 electron: 1
1 CH2 provides 1 electron: 1
Subtract 1 for π electron: -1
Total: 6 electrons
divide by 2 to give pairs: 3 electron pairs
3 electron pairs: trigonal geometry
3 bond pairs: so 0 lone pairs
Shape: trigonal
Example 8. SF3N
Lewis structure of SF3N and the calculation:VE on central atom: 6
3 F each provide 1 electron: 3
1 N provides 1 electron: 1
Subtract 2 for 2 π electrons: -2
Total: 8 electrons
divide by 2 to give pairs: 4 electron pairs
4 electron pairs: tetrahedral geometry
4 bond pairs: so 0 lone pairs
shape: tetrahedral.
Another assumptions that we also need to use in our VSEPR that is about space requirement. In VSEPR calculation we assume that lone pairs occupy more space than bonding in electron pairs and double bonds occupy more space than single bonds.
Example 9. [ClO4]−
lewis structure of [ClO4]− and the calculation:
central atom: Cl
VE on central atom: 7
4 O each provide 1 electron: 4
Subtract 4 for 4 π electrons: -4
Add 1 for negative charge: 1
Total: 8 electrons
divide by 2 to give pairs: 4 electron pairs
4 electron pairs: tetrahedral geometry
4 bond pairs: so 0 lone pairs
shape: tetrahedral.
Therefore, we can redraw [ClO4]− as tetrahedral below.
Example 10. ClF3
lewis structure of ClF3 and the calculation:central atom: Cl
VE on central atom: 7
3 F each provide 1 electron: 3
Total: 10 electrons
divide by 2 to give pairs: 5 electron pairs
5 electron pairs: trigonal bipyramidal geometry
3 bond pairs: so 2 lone pairs
In this case, the shape of ClF3 need a little bit consideration about the positions for lone pairs. From the calculation, it indicates a trigonal bipyramidal structure with three bonding pairs and two lone pairs, so the big question is where to place the lone pairs. There are three possibilities to put two lone pairs in this molecule as shown below.
The first thing we need to consider is lone pairs occupy more angular space and are located closer to their atoms than bond pairs. Hence, the interactions between two lone pairs at any given angle are greater than the interactions between two bonding pairs. The interaction between a lone pair and a bonding pair is somewhere in between. Any given structure will adopt a configuration in which interactions between electron pairs are minimised. To determine the geometry of ClF3, let tabulate those there structures based on the angle.
The first step to determine the geometry of ClF3 is to ignore all interactions at angles greater than 90° then cancelling 3 bp-lp as all the structure has 3 bp-lp. Hence, we have our new table as follow.
Example 11. NO2
lewis structure of NO2 and the calculation:VE on central atom: 5
2 O provide 2 electron: 2
Subtract 2 for 2 π electrons: -2
Total: 5 electrons
divide 2 to give pairs: 2.5 electron pairs
"3" electron pairs: trigonal geometry
2 bond pairs: so "1" lone pair
Shape: bent
For NO2 there is an integral number of electrons but a non-integral number of electron pairs as 2.5 electron pairs must be placed into three orbitals. Hence, the "lone pair" orbital is only "half filled", the O-N-O angle opens (to 134.1°) from the ideal angle of 120°.
Until this far, we only encounter the geometry up to 6 electron pairs, but molecules can have higher electron pairs such as 7 electron pairs which has two possible geometries. The first possible is undistorted pentagonal bipyramidal and the example is IF7. The other possibility is monocapped octahedron, such as XeF6 which 6 bonding pairs and 1 one lone pair. Distorted octahedron sometimes described as monocapped octahedron (lone pair in the capping position).
 |
| Pentagonal bipyramid (left) and monocapped octahedral (right) |
 |
| Square antiprism |
Comments